從非藝術學科談跨領域美感教育課程：數學篇

國立臺灣師範大學電機工程學系 賴以威副教授

一、前言

推廣數學科普時，我們常引用古希臘數學家畢達哥拉斯的名言「萬物皆數」，伽利略也曾說過，大自然是一本用數學寫成的書。數學是一種語言，既然是語言，便能描述一切事物，既然能描述一切事物，自然無所不在。不過，有趣的是當我們在推廣數學，想辦法讓數學變得有趣時，我們四處尋找不同的主題：科技、歷史、自然……尋尋覓覓後，驀然發現跟數學最契合的，就是藝術領域。或是說，就算是數學與科技的結合，數學與自然的結合，我們的跨域課程不管怎麼設計，都會刻意放入數學元素，而就算不刻意，最終也常常都會與藝術結合。以我自己來說，我也間接因為數學，認識了更多藝術，教學相長，從許多藝術領域師長身上學到了許多。

在本篇文章裡，我們會先舉幾個由本團隊臺師大新創教育企業數感實驗室，所開發的跨域課程。透過幾個實例，分享我們從數學切入所設計的跨域美感教育課程；其次，我們將會介紹這樣的數學跨域美感課程，對數學學習的幫助；再來，我們將介紹另一套課程模組：排笛；最後則是結論。

二、數學跨域美感教育課程

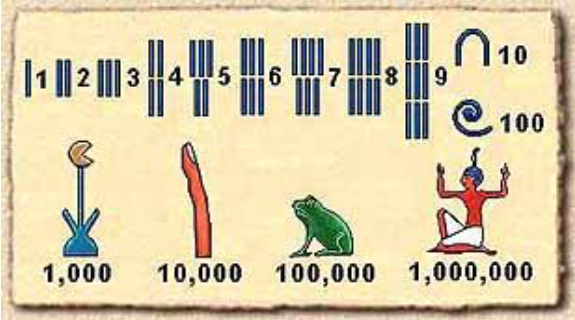
數感實驗室致力於讓數學「好用、好玩、好學」。為了達成此目標，我們團隊嘗試了多元的推廣方式，經營臉書粉絲頁、拍攝YouTube影片，甚至在2021年策畫了一套移動式數學展「環遊世界」。因應covid-19疫情下全球停止移動，我們選擇了埃及、法國、荷蘭等國家為主題，透過數學之眼來看這些國家。比方說，當飛機降落到埃及（我們用旅行作為整個展覽的主題），我們會看到埃及的石板，接著就會跟同學討論石板上的埃及象形文字，那其實是代表了1、10、100等各種十進位數字的符號。

來到法國，我們走到巴黎聖母院，教堂上經典的玫瑰窗是幾何與對稱的數學藝術結晶。透過互動機臺的攝影機，系統會擷取學生身上衣服的顏色，搭配手勢選擇，就能做出專屬於它自己的玫瑰窗。到了荷蘭，我們則是介紹錯視藝術大師艾雪，他雖然沒受過數學的訓練，卻因為家人的影響，讀過許多數學家的論文與書籍，包括由數學教育學家波利亞所撰寫的經典著作《如何解題》。艾雪的畫作充滿濃厚的數學氣息，他甚至在1954年受邀，在國際數學家大會舉辦個人畫展。當時，有一位名叫潘洛斯的學生看了畫展，深受吸引，進而跟艾雪結成了忘年之交。而這位潘洛斯，後來在物理與數學上有著卓越的貢獻，於2020年獲得諾貝爾物理獎。潘洛斯所創作的潘洛斯三角形、潘洛斯階梯等，後來也成為流行文化元素，在許多作品如電影《全面啟動》中都可以看見其蹤影。規劃環遊世界數學移動展時，我們是以旅行為主題，世界各地發想。然而，很自然而然的許多題材變成了數學與藝術的跨域結合。

回到課程發展上，我們團隊所開發的第一堂課「伊斯蘭窗花」也是數學跨域美感教育。在這門課中，我們的重點是數學知識裡的「比」，亦即兩組數字所形成的關係。簡單的說，一張照片不管是在手機上觀看，電腦螢幕上看，或是用投影機打在大投影屏幕上看，只要設定正確，照片裡的人物或景色就不會被壓縮或拉長。而所謂的設定正確，即是照片的「長寬比」維持定值，例如16:9、16:10、或是4:3。比的重點不在於數字的絕對值大小，不在於螢幕尺寸多少，而在於彼此的關係。

另一方面，伊斯蘭宗教文化中不允許偶像崇拜。因此，伊斯蘭教徒在信仰中逐漸發展出各式各樣的抽象幾何圖案。他們認為，如果能做出無窮無盡反覆的幾何圖案，一方面既能象徵神明之力無窮無盡，同時也代表了教徒對神明的信仰無窮無盡。幾何圖案所呈現的秩序、規律、反覆之美，則成了伊斯蘭教的重要象徵。這樣的幾何圖案繪製需要多種數學能力，對稱、鑲嵌、對各種幾何形狀的精熟。而幾何形狀中就牽扯到許多長寬比，或是長短對角線的比。我們在介紹完數學上的比，以螢幕這樣生活化的情境開場後，後面就會以伊斯蘭圖案為主，探討作品中用到的形狀的比。最後還會讓孩子親手設計、以玻璃紙跟鏤空紙板來製作一個專屬他們的伊斯蘭窗花。

如同前述，伊斯蘭窗花中的數學非常多元，因此本門課程如今已有多種版本，適用於不同階段的學生，數學知識將可從「比」改成「鑲嵌」、或是「幾何形狀」等等。我們的設計脈絡也從原本以數學知識出發，後續的改編都變成以伊斯蘭窗花這個藝術主題為核心，去發展出不同的數學課程。而不管是哪一種版本，藝術都佔了相當的課程比重。

三、結合美感教育，對數學課的幫助

我們稱這樣有主題性，結合手作的課程為「數學實驗課」，代表不只有生物、理化才有實驗課，數學也有實驗課。有趣的是，此課程名稱當初是家父所提。我的父親是小學老師，原本是文科背景，讀了許多數學科普書籍後，開始從事相關推廣。他在我高中時曾問過我：「數學為什麼沒有實驗課？」當時我無法理解這個問題，只認為數學是一門用紙筆就可以思考與學習的科目，能輕鬆一點當然好，幹嘛要跑去做多餘的實驗。

然而，隨著我也參與數學科普推廣後，我們發現，雖然數學課只需要紙筆，但不代表數學課就一定只能用紙筆。對一個觀念的感受，也會因為學習的方式不同而有所差異，就好比一個文本以小說、電影、遊戲等方式呈現時，受眾會有不同感受一樣。數學實驗課雖然看似繞遠路，將原本只需要簡單寫黑板、練習題就可以解釋完的觀念，用一個複雜的活動來呈現，但它同時提供了學生不一樣的學習體驗，將抽象的觀念具象化，讓孩子可以動手操作、感受到數學的實用性與威力（原來複雜的伊斯蘭圖案可以靠簡單的幾個形狀，搭配正確的對稱軸就能產生）。

而藝術，我們發現是最容易讓數學概念附著於之上，呈現抽象數學觀念的主題。

四、結合的方法：排笛

數感實驗室的YouTube頻道中有一個名為「數學實驗課」的撥放清單，現有15部影片，都是在介紹我們開發的動手做數學主題，內容多元如密碼筒、曲線刺繡、五邊形燈籠、六邊形翻翻驚喜卡、迷宮……，影片同時會附上我們設計的手作模板，提供老師自由運用。這是目前我們相當有效的數學推廣模式。

在本段，我們將特別介紹「排笛」這個結合音樂與數學的主題。相傳，前所述的古希臘數學家畢達哥拉斯有一天經過鐵匠鋪，發現鐵匠敲打不同長度的鐵條，即發出不同音高的聲響。畢達哥拉斯不僅研究數學，更信奉數學，而且深信一切都可以用簡單的整數比來描述。剛好，他發現鐵條長度是1：2與2:3這樣的簡單整數比時，所敲出來的音很悅耳。運用這兩個比，他發展出「畢氏音階」。

到這邊為止，都是我們在數學科普書中會看到的內容。書中接下來會介紹如何算出每個音，以及音階後續的演化和其對應的數學知識。而我們想做的，就是將這個知識具象化，真的去利用隨手可得的吸管，搭配黏土、膠帶，做出一個可吹奏的排笛樂器。在整堂課的規劃中，我們會帶著學生先了解畢達哥拉斯的設計原則，接著請他們按照手邊的吸管長度，計算各該剪掉多少長度，才能做出一副排笛。雖然看起來只用到1:2與2:3這兩個簡單整數比，應該不會太難。但實際上由於在設計時，需要交錯使用，幾次相乘後數字會變得更加複雜，就連七年級學生也需要一定程度的引導與提示，才能設計出正確的排笛。而如同伊斯蘭窗花的例子，我們在實際上課時可以看見，過去進入到繁瑣計算的部分時，會有一部分的學生選擇放棄。但當學生們知道計算是為了能做出一個可吹奏的排笛，甚至在某些班級老師會舉辦數學排笛音樂會時，參與的比例將大幅提高。英國數學家西爾維斯特（James Joseph Sylvester）曾說過：「難道不能形容音樂是數學的感性，而數學是音樂的理性？（May not music be described as the mathematics of the sense, mathematics as music of the reason?）」我們在好幾次上課時，看到了音樂與數學，感性與理性的交融。

五、總結

每隔四年一次的國際數學及科學趨勢調查（Trends in international Mathematics and Science Study：TIMSS）中，臺灣學生在數學學習成就上都是名列前茅，然而，若是問起臺灣學生對於數學的興趣、信心，則相對偏低，甚至有幾次調查來到了全球最低。以2019年的調查為例，當時的4年級臺灣學生各有44%對學好數學沒信心，41%對數學沒興趣。參與調查的全體4年級學生不喜歡數學與對數學沒信心的比例則只有約2成。換句話說，對數學持負面態度的臺灣孩子，是其他國家的兩倍之多。而這也是我與我們團隊一直在努力的目標。

數學跨域美感教育的數學實驗課，是我們在各種嘗試後發現的一個好方向，讓孩子看見不同的數學風景，稍微離開反覆的解題程序，感受藝術家為了完成作品需要的思考，以及其所運用的數學理性邏輯。也讓孩子看見彷彿數學與藝術這彷彿在光譜兩端的知識領域，當我們跳脫到更高維度時，光譜的頭尾即可銜接在一起，激盪出不一樣的火花。

目前數學實驗課的推展，不僅限於我們團隊辦理活動，也陸續與許多學校、教師展開合作，將課程模組以師培跟授權的方式，更全面的擴散。以110年第一學期為例，即有約2000名學生上過至少一門數學實驗課。這樣的推展即足以證明，不僅是我們，許多第一線的數學教師也認同數學跨域美感教育課程的價值。在傳遞知識上，這或許不是最有效率的方式，但考慮到因為趣味與參與度帶來的學習主動性，或許繞遠路，反而能走得更快。